斯坦福CS231n项目实战(四):浅层神经网络

我的微信公众号:红色石头的机器学习之路
神经网络(Neural Network)是一种非线性分类器,有别于之前介绍的线性分类器SVM和Softmax,更复杂一些。最简单的多分类浅层神经网络结构示例如下:
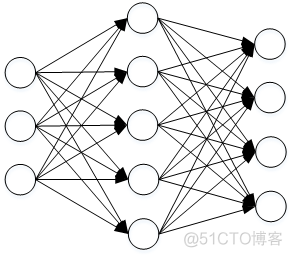
神经网络整个过程分为:正向传播和反向传播。正向传播时,隐藏层每个神经元都类似一个线性分类器,经过ReLU激活函数,所有隐藏层的神经元再进入到输出层,经过Softmax选择概率最大的标签作为预测分类值。反向传播时,利用梯度下降算法,计算Loss对应的各个层下权重W和常数项b的梯度。一般方法是根据计算图(Computional Graph),利用链式法则计算梯度:
∂f∂x=∂f∂q⋅∂q∂x ∂ f ∂ x = ∂ f ∂ q ⋅ ∂ q ∂ x
以函数f(x)=11+exp(−(w0x0+w1x1+w2)) f ( x ) = 1 1 + e x p ( − ( w 0 x 0 + w 1 x 1 + w 2 ) ) 为例,介绍一下计算图:

计算图中,绿色表示正向传播过程,红色表示反向传播求解梯度过程。
关于浅层神经网络,我在之前的笔记有过详细介绍:Coursera吴恩达《神经网络与深度学习》课程笔记(4)– 浅层神经网络
这里就不赘述了。
下面是浅层神经网络的实例代码,本文详细代码请见我的:
- Github
- 码云
1. Download the CIFAR10 datasets, and load it
# Load the raw CIFAR-10 data.
cifar10_dir = 'CIFAR10/datasets/cifar-10-batches-py'
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# As a sanity check, we print out the size of the training and test data.
print('Training data shape: ', X_train.shape)
print('Training labels shape: ', y_train.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
Training data shape: (50000, 32, 32, 3)
Training labels shape: (50000,)
Test data shape: (10000, 32, 32, 3)
Test labels shape: (10000,)
Show some CIFAR10 images
classes = ['plane', 'car', 'bird', 'cat', 'dear', 'dog', 'frog', 'horse', 'ship', 'truck']
num_classes = len(classes)
num_each_class = 7
for y, cls in enumerate(classes):
idxs = np.flatnonzero(y_train == y)
idxs = np.random.choice(idxs, num_each_class, replace=False)
for i, idx in enumerate(idxs):
plt_idx = i * num_classes + (y + 1)
plt.subplot(num_each_class, num_classes, plt_idx)
plt.imshow(X_train[idx].astype('uint8'))
plt.axis('off')
if i == 0:
plt.title(cls)
plt.show()

Subsample the data for more efficient code execution
# Split the data into train, val, test sets and dev sets
num_train = 49000
num_val = 1000
num_test = 1000
num_dev = 500
# Validation set
mask = range(num_train, num_train + num_val)
X_val = X_train[mask]
y_val = y_train[mask]
# Train set
mask = range(num_train)
X_train = X_train[mask]
y_train = y_train[mask]
# Test set
mask = range(num_test)
X_test = X_test[mask]
y_test = y_test[mask]
print('Train data shape: ', X_train.shape)
print('Train labels shape: ', y_train.shape)
print('Validation data shape: ', X_val.shape)
print('Validation labels shape ', y_val.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
Train data shape: (49000, 32, 32, 3)
Train labels shape: (49000,)
Validation data shape: (1000, 32, 32, 3)
Validation labels shape (1000,)
Test data shape: (1000, 32, 32, 3)
Test labels shape: (1000,)
2. Preprocessing
Reshape the images data into rows
# Preprocessing: reshape the images data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_val = np.reshape(X_val, (X_val.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
print('Train data shape: ', X_train.shape)
print('Validation data shape: ', X_val.shape)
print('Test data shape: ', X_test.shape)
Train data shape: (49000, 3072)
Validation data shape: (1000, 3072)
Test data shape: (1000, 3072)
Subtract the mean images
# Processing: subtract the mean images
mean_image = np.mean(X_train, axis=0)
X_train -= mean_image
X_val -= mean_image
X_test -= mean_image
3. Define a two-layer neural network
class TwoLayerNet(object):
def __init__(self, input_size, hidden_size, output_size, std = 1e-4):
"""
Initialize the model weights
W1: First layer weights; has shape (D, H)
b1: First layer biases; has shape (H,)
W2: Second layer weights; has shape (H, C)
b2: Second layer biases; has shape (C,)
Inputs:
- input_size: The dimension D of the input data.
- hidden_size: The number of neurons H in the hidden layer.
- output_size: The number of classes C.
"""
self.params = {}
self.params['W1'] = std * np.random.randn(input_size, hidden_size)
self.params['b1'] = np.zeros(hidden_size)
self.params['W2'] = std * np.random.randn(hidden_size, output_size)
self.params['b2'] = np.zeros(output_size)
def loss(self, X, y, reg = 0.0):
"""
Two-layer network loss function, vectorized implementation (without loops).
Inputs:
- X: A numpy array of shape (num_train, D) contain the training data
consisting of num_train samples each of dimension D
- y: A numpy array of shape (num_train,) contain the training labels,
where y[i] is the label of X[i]
- reg: float, regularization strength
Return:
- loss: the loss value between predict value and ground truth
- grads: Dictionary mapping parameter names to gradients of those parameters
with respect to the loss function; has the same keys as self.params.
Contain 'dW1', 'db1', 'dW2', 'db2'
"""
N, dim = X.shape
grads = {}
# input layer ==> hidden layer ==> ReLU ==> output layer ==> Softmax
W1 = self.params['W1']
b1 = self.params['b1']
W2 = self.params['W2']
b2 = self.params['b2']
# input layer==> hidden layer
Z1 = np.dot(X, W1) + b1
# hidden layer ==> ReLU
A1 = np.maximum(0, Z1) # ReLU function
# ReLU ==> output layer
scores = np.dot(A1, W2) + b2
# output layer ==> Softmax
scores_shift = scores - np.max(scores, axis=1).reshape(-1, 1)
Softmax_output = np.exp(scores_shift) / np.sum(np.exp(scores_shift), axis=1).reshape(-1, 1)
loss = -np.sum(np.log(Softmax_output[range(N), list(y)]))
loss /= N
loss += 0.5 * reg * np.sum(W1 * W1) + 0.5 * reg * np.sum(W2 * W2)
# grads
dS = Softmax_output.copy()
dS[range(N), list(y)] += -1
dS /= N
dW2 = np.dot(A1.T, dS)
db2 = np.sum(dS, axis=0)
dA1 = np.dot(dS, W2.T)
dZ1 = dA1 * (A1 > 0)
dW1 = np.dot(X.T, dZ1)
db1 = np.sum(dZ1, axis=0)
dW2 += reg * W2
dW1 += reg * W1
grads['W1'] = dW1
grads['b1'] = db1
grads['W2'] = dW2
grads['b2'] = db2
return loss, grads
def predict(self, X):
"""
Use the trained weights to predict data labels
Inputs:
- X: A numpy array of shape (num_test, D) contain the test data
Outputs:
- y_pred: A numpy array, predicted labels for the data in X
"""
W1 = self.params['W1']
b1 = self.params['b1']
W2 = self.params['W2']
b2 = self.params['b2']
Z1 = np.dot(X, W1) + b1
A1 = np.maximum(0, Z1) # ReLU function
scores = np.dot(A1, W2) + b2
y_pred = np.argmax(scores, axis=1)
return y_pred
def train(self, X, y, X_val, y_val, learning_rate=1e-3, learning_rate_decay=0.95,
reg=5e-6, num_iters=100, batch_size=200, print_flag=False):
"""
Train Two-layer neural network classifier using SGD
Inputs:
- X: A numpy array of shape (num_train, D) contain the training data
consisting of num_train samples each of dimension D
- y: A numpy array of shape (num_train,) contain the training labels,
where y[i] is the label of X[i], y[i] = c, 0 <= c <= C
- X_val: A numpy array of shape (num_val, D) contain the validation data
consisting of num_val samples each of dimension D
- y_val: A numpy array of shape (num_val,) contain the validation labels,
where y_val[i] is the label of X_val[i], y_val[i] = c, 0 <= c <= C
- learning rate: (float) learning rate for optimization
- learning_rate_decay: Scalar giving factor used to decay the learning rate
after each epoch.
- reg: (float) regularization strength
- num_iters: (integer) numbers of steps to take when optimization
- batch_size: (integer) number of training examples to use at each step
- print_flag: (boolean) If true, print the progress during optimization
Outputs:
- a dictionary contains the loss_history, train_accuracy_history and val_accuracy_history
"""
num_train = X.shape[0]
iterations_per_epoch = max(num_train / batch_size, 1)
loss_history = []
train_accuracy_history = []
val_accuracy_history = []
for t in range(num_iters):
idx_batch = np.random.choice(num_train, batch_size, replace=True)
X_batch = X[idx_batch]
y_batch = y[idx_batch]
loss, grads = self.loss(X_batch, y_batch, reg)
loss_history.append(loss)
self.params['W1'] += -learning_rate * grads['W1']
self.params['b1'] += -learning_rate * grads['b1']
self.params['W2'] += -learning_rate * grads['W2']
self.params['b2'] += -learning_rate * grads['b2']
# Every epoch, check train and val accuracy and decay learning rate.
if t % iterations_per_epoch == 0:
train_accuracy = np.mean(self.predict(X_batch) == y_batch)
val_accuracy = np.mean(self.predict(X_val) == y_val)
train_accuracy_history.append(train_accuracy)
val_accuracy_history.append(val_accuracy)
# Decay learning rate
learning_rate *= learning_rate_decay
# print the progress during optimization
if print_flag and t%100 == 0:
print('iteration %d / %d: loss %f' % (t, num_iters, loss))
return {
'loss_history': loss_history,
'train_accuracy_history': train_accuracy_history,
'val_accuracy_history': val_accuracy_history,
}
4. Stochastic Gradient Descent
input_size = 32 * 32 * 3
hidden_size = 50
num_classes = 10
net = TwoLayerNet(input_size, hidden_size, num_classes)
# Train the network
stats = net.train(X_train, y_train, X_val, y_val,
num_iters=1000, batch_size=200,
learning_rate=1e-4, learning_rate_decay=0.95,
reg=0.25, print_flag=True)
# Predict on the validation set
val_acc = (net.predict(X_val) == y_val).mean()
print('Validation accuracy: ', val_acc)
iteration 0 / 1000: loss 2.302782
iteration 100 / 1000: loss 2.302411
iteration 200 / 1000: loss 2.299242
iteration 300 / 1000: loss 2.272836
iteration 400 / 1000: loss 2.207163
iteration 500 / 1000: loss 2.081039
iteration 600 / 1000: loss 2.102869
iteration 700 / 1000: loss 2.099161
iteration 800 / 1000: loss 2.041299
iteration 900 / 1000: loss 2.010855
Validation accuracy: 0.286
# Plot the loss_history
plt.figure(figsize=(10,12))
plt.subplot(2, 1, 1)
plt.plot(stats['loss_history'])
plt.title('loss history')
plt.xlabel('Iteration number')
plt.ylabel('loss value')
# Plot the train_accuracy_history & val_accuracy_history
plt.subplot(2, 1, 2)
plt.plot(stats['train_accuracy_history'], label='train')
plt.plot(stats['val_accuracy_history'], label='val')
plt.title('Classification accuracy history')
plt.xlabel('Epoch')
plt.ylabel('Clasification accuracy')
plt.legend()
plt.show()

5. Tune your hyperparameters
# Hyperparameters
learning_rates = [1e-4, 5e-4, 9e-4, 13e-4, 15e-4]
regularization_strengths = [0.25, 0.5, 0.75, 1.0]
num_iters = 3000
batch_size = 200
learning_rate_decay = 0.98
# Net structure
input_size = 32 * 32 * 3
hidden_size = [50, 100, 150]
num_classes = 10
# Initialization
best_net = None
best_hidden_size = None
best_val = -1
best_lr = None
best_reg = None
results = {}
# Train the two layers network
for i in range(len(hidden_size)):
for lr in learning_rates:
for reg in regularization_strengths:
net = TwoLayerNet(input_size, hidden_size[i], num_classes)
stats = net.train(X_train, y_train, X_val, y_val,
num_iters=num_iters, batch_size=batch_size,
learning_rate=lr, learning_rate_decay=learning_rate_decay,
reg=reg, print_flag=False)
train_accuracy = stats['train_accuracy_history'][-1]
val_accuracy = stats['val_accuracy_history'][-1]
if val_accuracy > best_val:
best_lr = lr
best_reg = reg
best_val = val_accuracy
best_net = net
best_hidden_size = hidden_size[i]
results[(lr, reg)] = train_accuracy, val_accuracy
print('hidden_size: %d lr: %e reg: %e train accuracy: %f val accuracy: %f' %
(hidden_size[i], lr, reg, results[(lr, reg)][0], results[(lr, reg)][1]))
print('Best hidden_size: %d\nBest lr: %e\nBest reg: %e\ntrain accuracy: %f\nval accuracy: %f' %
(hidden_size[i], best_lr, best_reg, results[(best_lr, best_reg)][0], results[(best_lr, best_reg)][1]))
hidden_size: 50 lr: 1.000000e-04 reg: 2.500000e-01 train accuracy: 0.410000 val accuracy: 0.407000
hidden_size: 50 lr: 1.000000e-04 reg: 5.000000e-01 train accuracy: 0.415000 val accuracy: 0.399000
hidden_size: 50 lr: 1.000000e-04 reg: 7.500000e-01 train accuracy: 0.370000 val accuracy: 0.400000
hidden_size: 50 lr: 1.000000e-04 reg: 1.000000e+00 train accuracy: 0.420000 val accuracy: 0.403000
hidden_size: 50 lr: 5.000000e-04 reg: 2.500000e-01 train accuracy: 0.595000 val accuracy: 0.494000
hidden_size: 50 lr: 5.000000e-04 reg: 5.000000e-01 train accuracy: 0.595000 val accuracy: 0.505000
hidden_size: 50 lr: 5.000000e-04 reg: 7.500000e-01 train accuracy: 0.495000 val accuracy: 0.483000
hidden_size: 50 lr: 5.000000e-04 reg: 1.000000e+00 train accuracy: 0.600000 val accuracy: 0.475000
hidden_size: 50 lr: 9.000000e-04 reg: 2.500000e-01 train accuracy: 0.670000 val accuracy: 0.496000
hidden_size: 50 lr: 9.000000e-04 reg: 5.000000e-01 train accuracy: 0.675000 val accuracy: 0.510000
hidden_size: 50 lr: 9.000000e-04 reg: 7.500000e-01 train accuracy: 0.610000 val accuracy: 0.485000
hidden_size: 50 lr: 9.000000e-04 reg: 1.000000e+00 train accuracy: 0.635000 val accuracy: 0.487000
hidden_size: 50 lr: 1.300000e-03 reg: 2.500000e-01 train accuracy: 0.700000 val accuracy: 0.486000
hidden_size: 50 lr: 1.300000e-03 reg: 5.000000e-01 train accuracy: 0.590000 val accuracy: 0.500000
hidden_size: 50 lr: 1.300000e-03 reg: 7.500000e-01 train accuracy: 0.615000 val accuracy: 0.466000
hidden_size: 50 lr: 1.300000e-03 reg: 1.000000e+00 train accuracy: 0.620000 val accuracy: 0.481000
hidden_size: 50 lr: 1.500000e-03 reg: 2.500000e-01 train accuracy: 0.660000 val accuracy: 0.485000
hidden_size: 50 lr: 1.500000e-03 reg: 5.000000e-01 train accuracy: 0.585000 val accuracy: 0.466000
hidden_size: 50 lr: 1.500000e-03 reg: 7.500000e-01 train accuracy: 0.655000 val accuracy: 0.483000
hidden_size: 50 lr: 1.500000e-03 reg: 1.000000e+00 train accuracy: 0.630000 val accuracy: 0.484000
hidden_size: 100 lr: 1.000000e-04 reg: 2.500000e-01 train accuracy: 0.325000 val accuracy: 0.413000
hidden_size: 100 lr: 1.000000e-04 reg: 5.000000e-01 train accuracy: 0.340000 val accuracy: 0.416000
hidden_size: 100 lr: 1.000000e-04 reg: 7.500000e-01 train accuracy: 0.375000 val accuracy: 0.421000
hidden_size: 100 lr: 1.000000e-04 reg: 1.000000e+00 train accuracy: 0.480000 val accuracy: 0.409000
hidden_size: 100 lr: 5.000000e-04 reg: 2.500000e-01 train accuracy: 0.605000 val accuracy: 0.496000
hidden_size: 100 lr: 5.000000e-04 reg: 5.000000e-01 train accuracy: 0.580000 val accuracy: 0.510000
hidden_size: 100 lr: 5.000000e-04 reg: 7.500000e-01 train accuracy: 0.605000 val accuracy: 0.496000
hidden_size: 100 lr: 5.000000e-04 reg: 1.000000e+00 train accuracy: 0.540000 val accuracy: 0.508000
hidden_size: 100 lr: 9.000000e-04 reg: 2.500000e-01 train accuracy: 0.720000 val accuracy: 0.509000
hidden_size: 100 lr: 9.000000e-04 reg: 5.000000e-01 train accuracy: 0.665000 val accuracy: 0.507000
hidden_size: 100 lr: 9.000000e-04 reg: 7.500000e-01 train accuracy: 0.630000 val accuracy: 0.512000
hidden_size: 100 lr: 9.000000e-04 reg: 1.000000e+00 train accuracy: 0.610000 val accuracy: 0.497000
hidden_size: 100 lr: 1.300000e-03 reg: 2.500000e-01 train accuracy: 0.720000 val accuracy: 0.495000
hidden_size: 100 lr: 1.300000e-03 reg: 5.000000e-01 train accuracy: 0.775000 val accuracy: 0.524000
hidden_size: 100 lr: 1.300000e-03 reg: 7.500000e-01 train accuracy: 0.640000 val accuracy: 0.503000
hidden_size: 100 lr: 1.300000e-03 reg: 1.000000e+00 train accuracy: 0.665000 val accuracy: 0.478000
hidden_size: 100 lr: 1.500000e-03 reg: 2.500000e-01 train accuracy: 0.650000 val accuracy: 0.516000
hidden_size: 100 lr: 1.500000e-03 reg: 5.000000e-01 train accuracy: 0.675000 val accuracy: 0.499000
hidden_size: 100 lr: 1.500000e-03 reg: 7.500000e-01 train accuracy: 0.635000 val accuracy: 0.493000
hidden_size: 100 lr: 1.500000e-03 reg: 1.000000e+00 train accuracy: 0.600000 val accuracy: 0.493000
hidden_size: 150 lr: 1.000000e-04 reg: 2.500000e-01 train accuracy: 0.410000 val accuracy: 0.420000
hidden_size: 150 lr: 1.000000e-04 reg: 5.000000e-01 train accuracy: 0.475000 val accuracy: 0.415000
hidden_size: 150 lr: 1.000000e-04 reg: 7.500000e-01 train accuracy: 0.385000 val accuracy: 0.422000
hidden_size: 150 lr: 1.000000e-04 reg: 1.000000e+00 train accuracy: 0.375000 val accuracy: 0.425000
hidden_size: 150 lr: 5.000000e-04 reg: 2.500000e-01 train accuracy: 0.605000 val accuracy: 0.524000
hidden_size: 150 lr: 5.000000e-04 reg: 5.000000e-01 train accuracy: 0.550000 val accuracy: 0.512000
hidden_size: 150 lr: 5.000000e-04 reg: 7.500000e-01 train accuracy: 0.565000 val accuracy: 0.511000
hidden_size: 150 lr: 5.000000e-04 reg: 1.000000e+00 train accuracy: 0.580000 val accuracy: 0.501000
hidden_size: 150 lr: 9.000000e-04 reg: 2.500000e-01 train accuracy: 0.635000 val accuracy: 0.526000
hidden_size: 150 lr: 9.000000e-04 reg: 5.000000e-01 train accuracy: 0.615000 val accuracy: 0.512000
hidden_size: 150 lr: 9.000000e-04 reg: 7.500000e-01 train accuracy: 0.655000 val accuracy: 0.523000
hidden_size: 150 lr: 9.000000e-04 reg: 1.000000e+00 train accuracy: 0.585000 val accuracy: 0.507000
hidden_size: 150 lr: 1.300000e-03 reg: 2.500000e-01 train accuracy: 0.745000 val accuracy: 0.519000
hidden_size: 150 lr: 1.300000e-03 reg: 5.000000e-01 train accuracy: 0.655000 val accuracy: 0.501000
hidden_size: 150 lr: 1.300000e-03 reg: 7.500000e-01 train accuracy: 0.625000 val accuracy: 0.530000
hidden_size: 150 lr: 1.300000e-03 reg: 1.000000e+00 train accuracy: 0.645000 val accuracy: 0.506000
hidden_size: 150 lr: 1.500000e-03 reg: 2.500000e-01 train accuracy: 0.660000 val accuracy: 0.478000
hidden_size: 150 lr: 1.500000e-03 reg: 5.000000e-01 train accuracy: 0.675000 val accuracy: 0.485000
hidden_size: 150 lr: 1.500000e-03 reg: 7.500000e-01 train accuracy: 0.670000 val accuracy: 0.512000
hidden_size: 150 lr: 1.500000e-03 reg: 1.000000e+00 train accuracy: 0.655000 val accuracy: 0.495000
Best hidden_size: 150
Best lr: 1.300000e-03
Best reg: 7.500000e-01
train accuracy: 0.625000
val accuracy: 0.530000
from vis_utils import visualize_grid
# Visualize the weights of the network
def show_net_weights(net):
W1 = net.params['W1']
W1 = W1.reshape(32, 32, 3, -1).transpose(3, 0, 1, 2)
plt.imshow(visualize_grid(W1, padding=3).astype('uint8'))
plt.gca().axis('off')
plt.show()
show_net_weights(net)

Run on the test set
test_acc = (best_net.predict(X_test) == y_test).mean()
print('Test accuracy: ', test_acc)
Test accuracy: 0.504
更多AI资源请关注公众号:红色石头的机器学习之路







