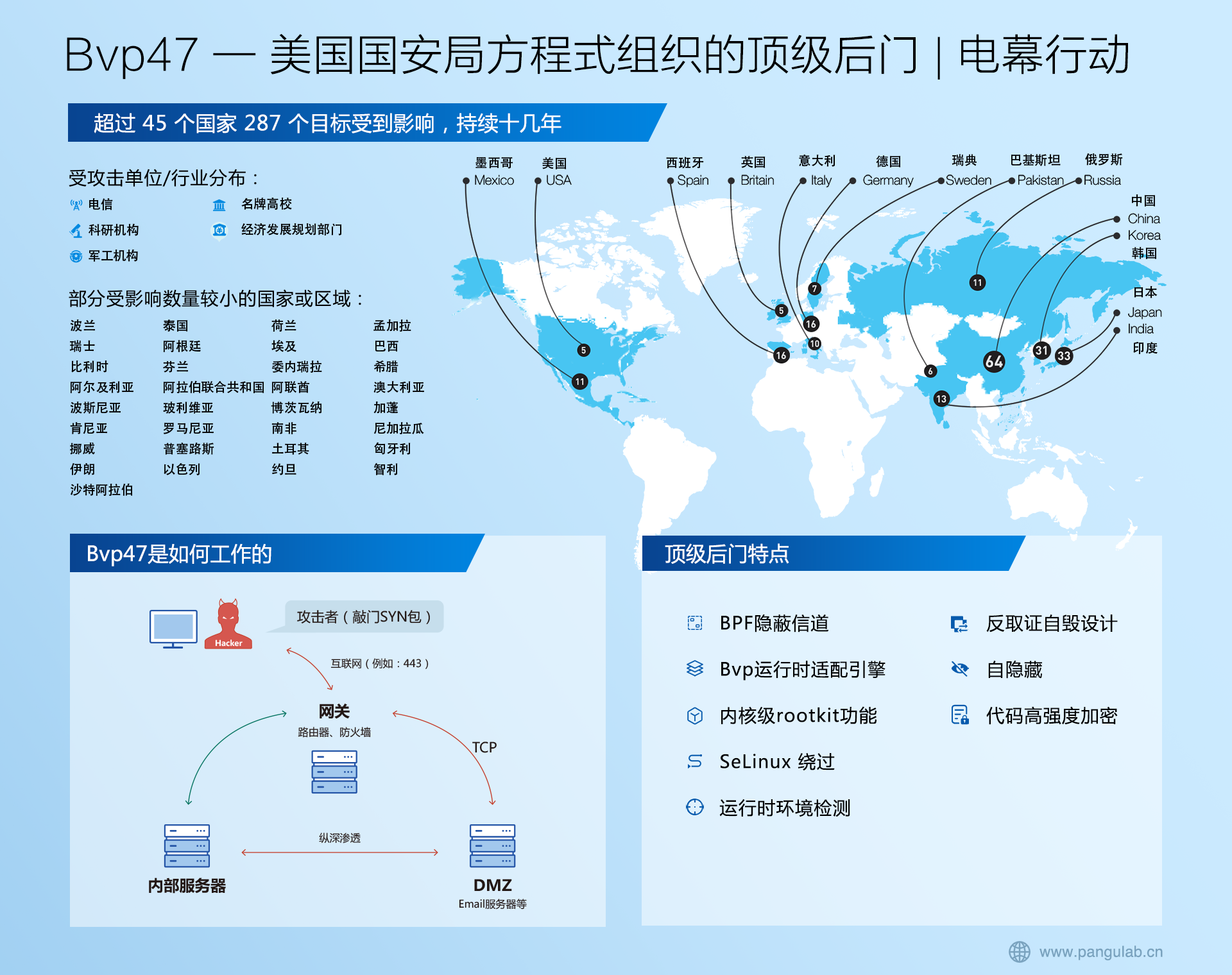
matlab计量经济学工具箱
Econometric Modeling
A simple model is easier to estimate, forecast, and interpret.
- Specification tests helps you identify one or more model families that could plausibly describe the data generating process.
- Model comparisons help you compare the fit of competing models, with penalties for complexity.
- Goodness-of-fit checks help you assess the in-sample adequacy of your model, verify that all model assumptions hold, and evaluate out-of-sample forecast performance.
- arima
- garch
- egarch
- gjr(s a variant of the GARCH conditional variance model, named for Glosten, Jagannathan, and Runkle)
A model object holds all the information necessary to estimate, simulate, and forecast econometric models.
- Parametric form of the model
- Number of model parameters (e.g., the degree of the model)
- Innovation distribution (Gaussian or Student's t)
- Amount of presample data needed to initialize the model
Example1: AR(2)
where the innovations are independent and identically distributed normal random variables with mean 0 and variance 0.2. This is a conditional mean model, so use arima.
>>model = arima('AR',{0.8,-0.2},'Variance',0.2,'Constant',0)
Example2: GARCH(1,1) model
>>model = garch('GARCH',NaN,'ARCH',NaN)
或者
>>model = garch(1,1)
Parameters with NaN values need to be estimated or otherwise specified before you can forecast or simulate the model.
To display the value of the property AR for the created variable object,
>>model.AR
>>model.Distribution = struct('Name','t','DoF',8)
Methods are functions that accept model objects as inputs. In Econometrics Toolbox,
- estimate
- infer
- forecast
- simulate
Example3: Fit an ARMA(2,1) model to simulated data
1) Simulate 500 data points from the ARMA(2,1) model
>>simModel = arima('AR',{0.5,-0.3},'MA',0.2,'Constant',0,'Variance',0.1);
>>rng(5);
>>Y = simulate(simModel,500);
2) Specify an ARMA(2,1) model with no constant and unknown coefficients and variance.
>>model = arima(2,0,1);
>>model.Constant = 0
3) Fit the ARMA(2,1) model to Y.
>>fit = estimate(model,Y)
Example4: infer
>>load Data_EquityIdx
>>nasdaq = Dataset.NASDAQ;
>>r = price2ret(nasdaq);
>>r0 = r(1:2);
>>rn = r(3:end);
Fit a GARCH(1,1) model to the returns, and infer the loglikelihood objective function value.
>>model1 = garch(1,1);
>>fit1 = estimate(model1,rn,'E0',r0);
>>[~,LogL1] = infer(fit1,rn,'E0',r0);
Wold's theorem: you can write all weakly stationary stochastic processes in the general linear form
,
Thus, by Wold's theorem, you can model(or closely approximate) every stationary stochastic process as
The conditional mean and variance models
Stationarity tests If your data is not stationary, consider transforming your data. Stationarity is the foundation of many time series models.
You can difference a series with a unit root until it is stationary, Or, consider using a nonstationary ARIMA model if there is evidence of a unit root in your data.
Seasonal ARIMA models use seasonal differencing to remove seasonal effects. You can also include seasonal lags to model seasonal autocorrelation.
Conduct a Ljung-Box Q-test to test autocorrelations at several lags jointly. If autocorrelation is present, consider using a conditional mean model.
Looking for autocorrelation in the squared residual series is one way to detect conditional
Heteroscedasticity. To model conditional heteroscedasticity, consider using a conditional variance model.
You can use a Student’s t distribution to model fatter tails than a Gaussian distribution (excess
kurtosis).
You can compare nested models using misspecification tests, such as the likelihood ratio test, Wald’s test, or Lagrange multiplier test.
The Johansen and Engle-Granger cointegration tests assess evidence of cointegration. Consider using the VEC model for modeling multivariate, cointegrated series. It can introduce spurious regression effects.
The example “Specifying Static Time Series Models” explores cointegration in static regression
models. Type >> showdemo Demo_StaticModels.
Why Transform?
- Isolate temporal components of interest.
- Remove the effect of nuisance components (like seasonality).
- Make a series stationary.
- Reduce spurious regression effects.
- Stabilize variability that grows with the level of the series.
- Make two or more time series more directly comparable.
P207
An example of a static conditional mean model is the ordinary linear regression model.
A dynamic conditional mean model specifies the evolution of the conditional mean, , Examples:
By Wold’s decomposition, you can write the conditional mean of any stationary process yt as
And is the constant unconditional mean of the stationary process.
arima(p,D,q): nonseasonal AR terms (p), the order of nonseasonal integration (D), and the number of nonseasonal MA terms (q).
When simulating time series models, one draw (or, realization) is an entire sample path of specified length N, y1, y2,...,yN, generate M sample paths, each of length N.
Some extensions of Monte Carlo simulation rely on generating dependent random draws, such as Markov Chain Monte Carlo (MCMC). The simulate method in Econometrics Toolbox generates independent realizations.
• Demonstrating theoretical results
• Forecasting future events
• Estimating the probability of future events
- Specifying any required presample data (or use default presample data).
- Generating an uncorrelated innovation series from the specified innovation distribution.
- Generating responses by recursively applying the specified AR and MA polynomial operators. The AR polynomial operator can include differencing.
• For stationary processes, presample responses are set to the unconditional mean of the process.
• For nonstationary processes, presample responses are set to zero.
• Presample innovations are set to zero.
Step 1. Specify a model.
>>model = arima('Constant',0.5,'AR',{0.7,0.25},'Variance',.1);
Step 2. Generate one sample path.
>>rng('default')
>>Y = simulate(model,50);
>>figure(1)
>>plot(Y)
>>xlim([0,50])
>>title('Simulated AR(2) Process')
Step 3. Generate many sample paths.
rng('default')
Y = simulate(model,50,'numPaths',1000);
figure(2)
subplot(2,1,1)
plot(Y,'Color',[.85,.85,.85])
title('Simulated AR(2) Process')
hold on
h=plot(mean(Y,2),'k','LineWidth',2);
legend(h,'Simulation Mean','Location','NorthWest')
hold off
subplot(2,1,2)
plot(var(Y,0,2),'r','LineWidth',2)
title('Process Variance')
hold on
plot(1:50,.83*ones(50,1),'k--','LineWidth',1.5)
legend('Simulation','Theoretical',...
'Location','SouthEast')
hold off
Step 4. Oversample the process.
To reduce transient effects, one option is to oversample the process, simulate paths of length 150, and discard the first 100 observations.
Step 1. Generate realizations from a trend-stationary process.
t = [1:200]';
trend = 0.5*t;
model = arima('Constant',0,'MA',{1.4,0.8},'Variance',8);
rng('default')
u = simulate(model,300,'numPaths',50);
Yt = repmat(trend,1,50) + u(101:300,:);
Step 2. Generate realizations from a difference-stationary process.
>>model = arima('Constant',0.5,'D',1,'MA',{1.4,0.8},'Variance',8);
• Volatility clustering. Volatility is the conditional standard deviation of a time series. Autocorrelation in the conditional variance process results in volatility clustering.
• Leverage effects. The volatility of some time series responds more to large decreases than to large increases. The EGARCH and GJR models have leverage terms to model this asymmetry.
GARCH Model
EGARCH Model
Step 1. Load the data.
Load the exchange rate data included with the toolbox.
load Data_MarkPound
Y = Data;
N = length(Y);
figure(1)
plot(Y)
set(gca,'XTick',[1,659,1318,1975]);
set(gca,'XTickLabel',{'Jan 1984','Jan 1986','Jan 1988',...
'Jan 1992'})
ylabel('Exchange Rate')
title('Deutschmark/British Pound Foreign Exchange Rate')
Step 2. Calculate the returns.
Convert the series to returns. This results in the loss of the first observation.
r = price2ret(Y);
figure(2)
plot(2:N,r)
set(gca,'XTick',[1,659,1318,1975]);
set(gca,'XTickLabel',{'Jan 1984','Jan 1986','Jan 1988',...
'Jan 1992'})
ylabel('Returns')
title('Deutschmark/British Pound Daily Returns')
Step 3. Check for autocorrelation.
Check the returns series for autocorrelation. Plot the sample ACF and PACF,
and conduct a Ljung-Box Q-test.
figure(3)
subplot(2,1,1)
autocorr(r)
subplot(2,1,2)
parcorr(r)
[h,p] = lbqtest(r,[5 10 15])
Step 4. Check for conditional heteroscedasticity.
figure(4)
subplot(2,1,1)
autocorr((r-mean(r)).^2)
subplot(2,1,2)
parcorr((r-mean(r)).^2)
[h,p] = archtest(r-mean(r),'lags',2)
Step 5. Specify a GARCH(1,1) model.
model = garch('Offset',NaN,'GARCHLags',1,'ARCHLags',1)
Step 1. Load the data.
Load the Danish nominal stock return data included with the toolbox.
load Data_Danish
Y = Dataset.RN;
N = length(Y);
figure(1)
plot(Y)
xlim([0,N])
title('Danish Nominal Stock Returns')
Step 2. Fit an EGARCH(1,1) model.
Specify, and then fit an EGARCH(1,1) model to the nominal stock returns
series. Include a mean offset, and assume a Gaussian innovation distribution.
model = egarch('Offset',NaN','GARCHLags',1,...
'ARCHLags',1,'LeverageLags',1);
fit = estimate(model,Y);
Step 3. Infer the conditional variances.
Infer the conditional variances using the fitted model.
V = infer(fit,Y);
figure(2)
plot(V)
xlim([0,N])
title('Inferred Conditional Variances')
Step 4. Compute the standardized residuals.
Compute the standardized residuals for the model fit. Subtract the estimated
mean offset, and divide by the square root of the conditional variance process.
res = (Y-fit.Offset)./sqrt(V);
figure(3)
subplot(2,2,1)
plot(res)
xlim([0,N])
title('Standardized Residuals')
subplot(2,2,2)
hist(res)
subplot(2,2,3)
autocorr(res)
subplot(2,2,4)
parcorr(res)
Resampling Statistics
Bootstrap Jackknife
The bootstrap procedure:each observation is selected separately at random from the original dataset.
>>load lawdata
>>plot(lsat,gpa,'+')
>>lsline
>>rhohat = corr(lsat,gpa)
though it may seem large, you still do not know if it is statistically significant.
Using the bootstrp function you can resample the lsat and gpa vectors as many times as you like and consider the variation in the resulting correlation coefficients.
>>rhos1000 = bootstrp(1000,'corr',lsat,gpa);
This command resamples the lsat and gpa vectors 1000 times and computes the corr function on each sample.
>>hist(rhos1000,30)
>>set(get(gca,'Children'),'FaceColor',[.8 .8 1])
Nearly all the estimates lie on the interval [0.4 1.0].
>>ci = bootci(5000,@corr,lsat,gpa)
to obtain a confidence interval under 95% .
The jackknife computes sample statistics on n separate samples of size n-1, Each sample is the original data with a single observation omitted.
You can use the jackknife to estimate the bias, which is the tendency of the sample correlation to over-estimate or under-estimate the true, unknown correlation.
>>jackrho = jackknife(@corr,lsat,gpa);
>>meanrho = mean(jackrho)
>>n = length(lsat);
>>biasrho = (n-1) * (meanrho-rhohat)
biasrho = -0.0065
The sample correlation probably underestimates the true correlation by about this amount.