C++不知算法系列之解析回溯算法中的人文哲学

1. 前言

回溯算法让我想起“退一步海阔天空”的名言。当事情的发展到了绝境或是边缘时，可以试着后退一步，换一个方向、换一种策略，或许会看到新的出路或生机。

回溯算法的精髓：无所畏惧而不固执，善于在变通中迂回。故回溯算法也可称为试探算法。

万事万物之间必然相通而有共性，曲径相通，优秀算法思想中必也有人文哲学的韵意，想来，回溯思想是有”车到山前必有路“的励志！

本文通过几个案例，和大家一起聊聊，颇具有人生哲学韵味的回溯算法。

2. 深入回溯

2.1 递归回溯框架

回溯算法的流程如同下棋：

“举棋不定”这句成语源于下棋，缘何如此？因为每一步都有多个选择，不到最后无法知道哪一个选择是最好的，因而不定。

回溯算法则告诉我们，勇敢走出每一步，确实走不下去了，后退一步，换一个选择。回溯的关键点是可以后退，但下棋是生活，定是“落棋无悔”的。

Tips：有“落棋无悔”，也有复盘一说，下完后，可以讨论某一步如果怎样，结果又会怎样。这便是回溯。

回溯是思想，递归是手段，归功于递归的特性，它能让回溯思想优雅地得以自由驰骋。当然，能让这种思想落地的手段远不止递归。

本文在实现案例中的回溯过程都借助递归实现。如果一类问题均能通过回溯算法解决，则问题的本质一定相同，或可以透过问题的表征看到他们其实都是一个模样。

递归回溯算法的框架一：

//搜索函数，参数往往是搜索的起点
int search(int k) 
{   
    //如同下棋，每一步都有多个选择，回溯说，没关系，从第一个选择开始吧！ 
	for(int i=1;i<=选择数;i++){
		if(满足条件){
            //如果选择可以，存储当前的选择，如同下棋，落子！
		   保存结果
		   if(搜索到目标){
              //如果胜利了，输出 
		   	 输出解 
		   } 
		   else
              //继续下一步 
		     search(k+1);
         //回溯的关键点，如同悔棋，起子，进入下次循环（重新选择）   
		回溯到上一步并且恢复状态	  
		} 
	}	
}

递归回溯算法框架二：

int search(int k){
	if (搜索到目的)
        输出解 
	else
        for (int i=l;i<=算符种数;i++)
        	if (满足条件)
               { 
        		search(k+ 1);
        		回溯一步,恢复保存结果之前的状态
               }
}

2.2 案例剖析

2.2.1 素数环

问题描述：把从1到20这20个数摆成一个环，要求相邻两个数的和是一个素数。如下图所示，要求第 1 个格间和最后 1 个格间是逻辑相连的。

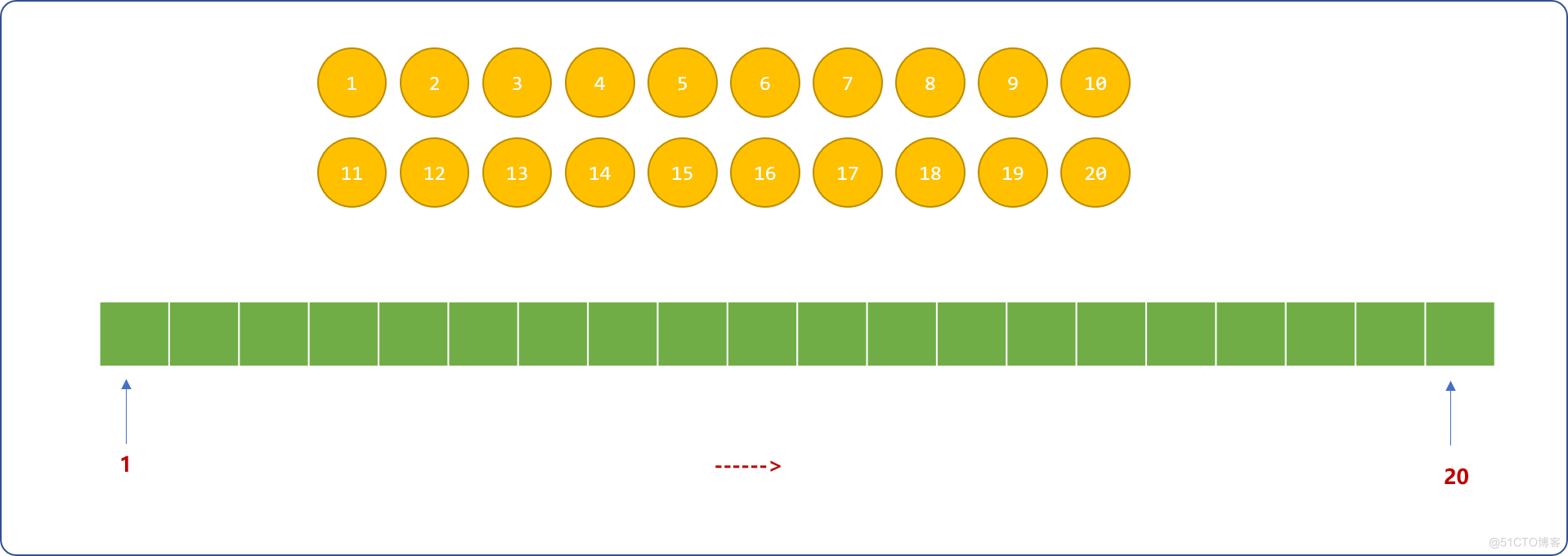
问题分析：任何问题的解决方案，绝对不止一种，但此问题绝对算得上是典型的回溯问题。

• 先在环的第 1个格间摆放数字 1。再从 2~20个数字中以试探的方法逐个选择，直到找到和左边数字相加为素数的数字，然后填充在第 2 个格间。

• 重复上述过程，继续在剩下的数字中选择一个符合条件的数字依次填充在环中空着的格间。如下为填到环中第 5 个格间时的演示图。

• 如下是填到环中第 12 个格间时的演示图。

• 如下是填充完环中第 19个格间后的演示图，环中还有最后一个格间，数字也只剩下 20。因为 20+19=39不是一个素数，20这个数字无法填充至第 20格间。至此，是回溯算法展示其魅力的时候。

• 回退到第 19个格间的填充，恢复 19数字的自由，重新选择 20这个数字。

• 第 20 个格间只能选择19数字，还是不满足要求。需再次后退至第 19个格间的填充，因为第 19个格间用完了所有选择，只能再后退到第 18个格间的填充且恢复填在第 18格间的数字18的自由。

• 如下图为第一种正确的填充方案。并不是一次性填充成功，而是经过多次回溯、再选择方能找到正确答案。得到答案后，第 20 个格间又可以释放填入的数字，重新选择数字或回溯到上一个格间，寻找其它的可行答案。

编程实现：

#include 
#include 
using namespace std;
//保存1~20范围内的所有数字
int nums[21]= {0};
//标记数字是否已经使用
bool isUse[21]= {0};
//存储结果
int res[21]= {0};
//所有的方案
int total=0;
/*
*初始化
*/
void init() {
	nums[0]=0;
	for(int i=1; i<=20; i++)
		nums[i]=i;
}
/*
* 判断给定的数字是不是素数
*/
bool isSs(int num ) {
	for(int i=2; i<=int( sqrt( num ) ) ; i++ ) {
		if(num % i==0)return false;
	}
	return true;
}
//打印填充方案
void show() {
	cout<<"------------------------"<

#include 
#include 
using namespace std;
//从 10 个数字中选择 5 个数字的所有排列
int nums[11]= {0};
//标记数字是否已经使用
bool isUse[11]= {0};
//排列个数
int total=0;
//选择的数字个数
int m=5; 
//存储结果
int res[5]= {0};
/*
*初始化
*/
void init() {
	nums[0]=0;
	for(int i=1; i<=10; i++)
		nums[i]=i;
}
//打印方案
void show() {
	cout<<"------------------------"<

#include 
#include 
using namespace std;
//存储结果 ，初始值为 1
int res[100]= {1};
//存储输入
int num;
//总个数
int total=0;
/*
*查找后，输入结果
*/
int print(int pos) {
	cout<>num;
	search(num,1);
	cout<

//省略，在搜索函数中修改 i 的起点
void search(int target,int pos ) {
	//每一个位置都有 1~target 个选择
	for(int i=res[pos-1]; i<=target; i++  ) {
		if(i==num)continue;
		res[pos]=i;
		target-=i;
		if(target==0)print(pos);
		else search(target,pos+1);
		target+=i;
	}
}
//省略……

#include 
#include 
#include 
using namespace std;
//二维数组，用来存储皇后位置
int nums[9][9]= {0};
//记数
int total=0;
int show() {
	total++;
	for(int i=1; i<9; i++) {
		for(int j=1; j<9; j++) {
			if( nums[i][j]!=0 ) {
				cout<<"("<=col  && (row-col)==(i-j)   &&    nums[i][j]!=0 )return false;
			if ( row